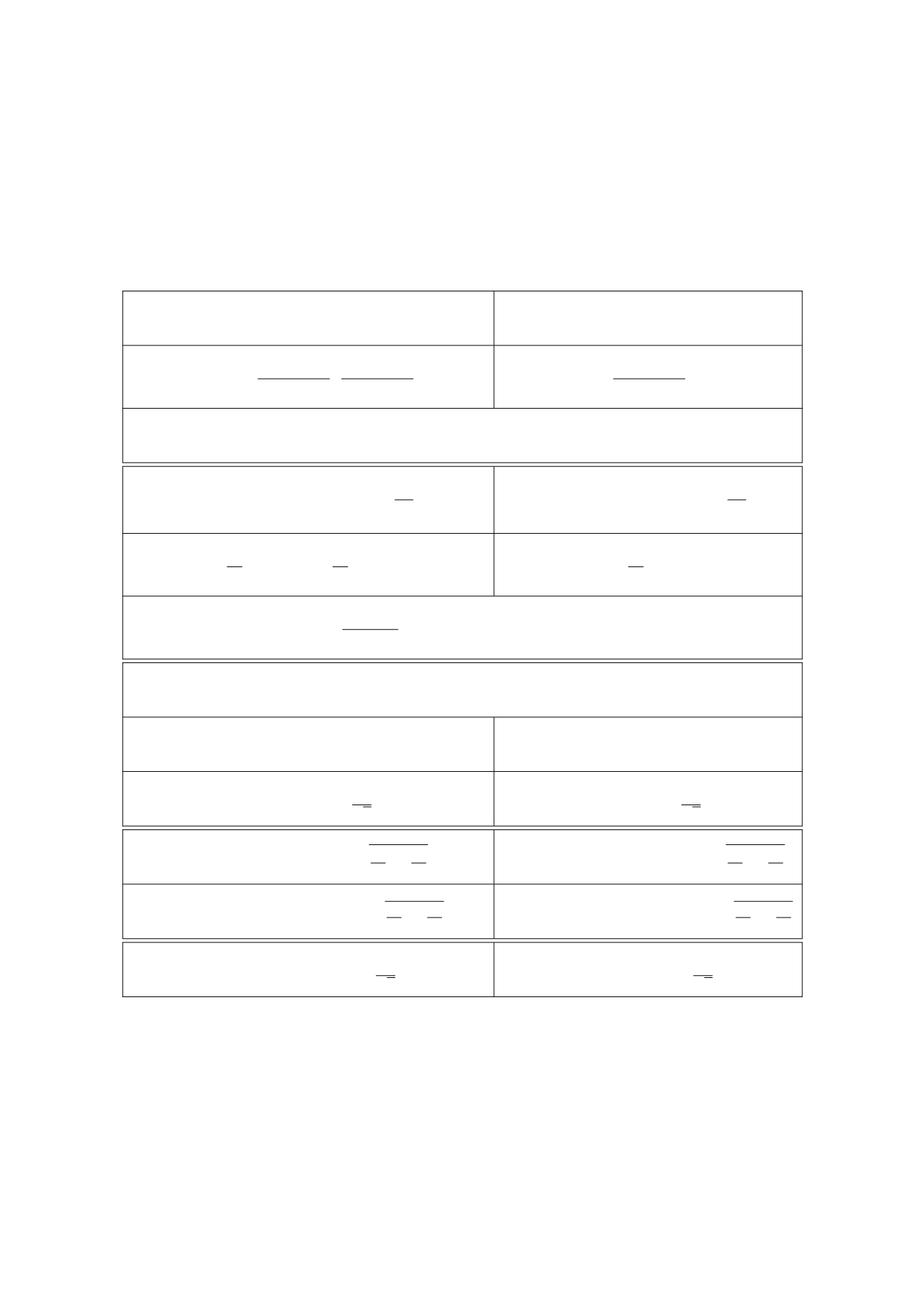
Confidence intervals for
σ
2
Hypothesis testing for
σ
2
(
n
−
1)
s
2
χ
2
α/
2
,ν
,
(
n
−
1)
s
2
χ
2
1
−
α/
2
,ν
χ
2
test
=
(
n
−
1)
s
2
σ
2
0
∼
χ
2
α,ν
where
ν
=
n
−
1
Confidence intervals for
σ
2
1
σ
2
2
Hypothesis testing for
σ
2
1
σ
2
2
s
2
1
s
2
2
f
1
−
α/
2
, ν
2
, ν
1
,
s
2
1
s
2
2
f
α/
2
, ν
2
, ν
1
f
test
=
s
2
1
s
2
2
∼
f
α, ν
1
, ν
2
f
1
−
α, ν
2
, ν
1
=
1
f
α, ν
1
, ν
2
where
ν
1
=
n
1
−
1
, ν
2
=
n
2
−
1
One-sided Confidence Interval for Lower and Upper Bound
One-sided Lower Bound
One-sided Upper Bound
µ >
¯
x
−
z
α
σ
√
n
µ <
¯
x
+
z
α
σ
√
n
µ
1
−
µ
2
>
(¯
x
1
−
¯
x
2
)
−
z
α
σ
2
1
n
1
+
σ
2
2
n
2
µ
1
−
µ
2
<
(¯
x
1
−
¯
x
2
) +
z
α
σ
2
1
n
1
+
σ
2
2
n
2
µ
1
−
µ
2
>
(¯
x
1
−
¯
x
2
)
−
z
α
s
p
1
n
1
+
1
n
2
µ
1
−
µ
2
<
(¯
x
1
−
¯
x
2
) +
z
α
s
p
1
n
1
+
1
n
2
µ
D
>
¯
x
D
−
z
α
σ
D
√
n
µ
D
<
¯
x
D
+
z
α
σ
D
√
n
7
Statistical Tables and Formulae 2.0








